Double and Triple Integrals

exercises

Question 5.74

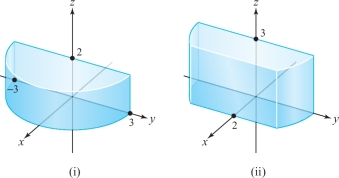
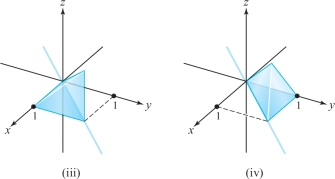
In parts (a) through (d) below, each iterated integral is an integral over a region \(D\). Match the integral with the correct region of integration.

(a) \(\displaystyle\int_{0}^{2} \int_{0}^{3} \int_{-\sqrt{9-x}}^{\sqrt{9-x}} \, {\it dy}\, {\it dz}\, {\it dx}\)
(b) \(\displaystyle\int_{0}^{2} \int_{0}^{3} \int_{-\sqrt{9-x^{2}}}^{\sqrt{9-x^{2}}} \, {\it dy}\, {\it dx}\, {\it dz}\)
(c) \(\displaystyle\int_{0}^{1} \int_{0}^{x} \int_{0}^{y} \, {\it dz}\, {\it dy}\, {\it dx}\)
(d) \(\displaystyle\int_{0}^{1} \int_{0}^{y} \int_{0}^{x} \, {\it dz}\, {\it dx}\, {\it dy}\)

Question 5.75

Evaluate the following triple integral: \[ \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} \sin x \, {\it dx}\, {\it dy}\, {\it dz}, \] where \(W\) is the solid given by \(0 \leq x \leq \pi\), \(0 \leq y \leq 1\), and \(0 \leq z \leq x\).

In Exercises 3 to 6, perform the indicated integration over the given box.

303

Question 5.76

\(\displaystyle\int\!\!\!\int\!\!\!\int_B x^2{\it dx}\,{\it dy}\,{\it dz},B=[0,1]\times [0,1]\times [0,1]\)

Question 5.77

\(\displaystyle\int\!\!\!\int\!\!\!\int_B e^{-xy}\,y\,{\it dx}\,{\it dy}\,{\it dz},B=[0,1]\times [0,1]\times [0,1]\)

Question 5.78

\(\displaystyle\int\!\!\!\int\!\!\!\int_B (2x+3y+z)\,{\it dx}\,{\it dy}\,{\it dz},B=[0,2]\times [-1,1]\times [0,1]\)

Question 5.79

\(\displaystyle\int\!\!\!\int\!\!\!\int_B ze^{x+y}{\it dx}\,{\it dy}\,{\it dz},B=[0,1]\times [0,1]\times [0,1]\)

In Exercises 7 to 10, describe the given region as an elementary region.

Question 5.80

The region between the cone \(z=\sqrt{x^2+y^2}\) and the paraboloid \(z=x^2+y^2\)

Question 5.81

The region cut out of the ball \(x^2+y^2+z^2\leq 4\) by the elliptic cylinder \(2x^2+z^2=1\); that is, the region inside the cylinder and the ball

Question 5.82

The region inside the sphere \(x^2+y^2 +z^2=1\) and above the plane \(z=0\)

Question 5.83

The region bounded by the planes \(x=0,y=0, z=0, x+y=4,\) and \(x=z-y-1\)

Find the volume of the region in Exercises 11 to 14.

Question 5.84

The region bounded by \(z=x^2+y^2\) and \(z=10-x^2-2y^2\)

Question 5.85

The solid bounded by \(x^2+2y^2=2,z=0\), and \(x+y+2z=2\)

Question 5.86

The solid bounded by \(x=y,z=0,y=0,x=1,\) and \(x+y+z=0\)

Question 5.87

The region common to the intersecting cylinders \(x^2+y^2\leq a^2\) and \(x^2+z^2\leq a^2\)

Evaluate the integrals in Exercises 15 to 23.

Question 5.88

\(\displaystyle\int^1_0\int^2_1\int^3_2 \cos\, [\pi(x+y+z)]\,{\it dx}\,{\it dy}\,{\it dz}\)

Question 5.89

\(\displaystyle\int^1_0\int^x_0\int^y_0 (y+xz)\,{\it dz}\,{\it dy}\,{\it dx}\)

Question 5.90

\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W (x^2+y^2+z^2)\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the region bounded by \(x+y+z=a\) (where \(a > 0\)), \(x=0,y=0\), and \(z=0\).

Question 5.91

\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W z\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the region bounded by the planes \(x=0,y=0,z=0,z=1,\) and the cylinder \(x^2+y^2=1\), with \(x\geq 0,y\geq 0\).

Question 5.92

\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W x^2\cos z{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the region bounded by \(z=0,z=\pi,y=0, y=1,x=0,\) and \(x+y=1\).

Question 5.93

\(\displaystyle\int^2_0\int^x_0\int^{x+y}_0{\it dz}\,{\it dy}\,{\it dx}\)

Question 5.94

\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W(1-z^2)\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the pyramid with top vertex at \((0,0,1)\) and base vertices at \((0,0,0)\), \((1,0,0)\), \((0,1,0),\) and \((1,1,0)\).

Question 5.95

\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W(x^2+y^2)\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the same pyramid as in Exercise 21.

Question 5.96

\(\displaystyle\int^1_0\int^{2x}_0\int^{x+y}_{x^2+y^2}{\it dz}\,{\it dy}\,{\it dx}.\)

Question 5.97

(a) Sketch the region for the integral \(\displaystyle\int^1_0\int^x_0\int^y_0 f(x,y,z)\,{\it dz}\,{\it dy}\,{\it dx}.\)
(b) Write the integral with the integration order \({\it dx}\,{\it dy}\,{\it dz}\).

For the regions in Exercises 25 to 28, find the appropriate limits \(\phi_1(x),\phi_2(x),\gamma_1(x,y),\) and \(\gamma_2(x,y),\) and write the triple integral over the region W as an iterated integral in the form \[ \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} f {\,d} V=\int^b_a \bigg\{ \int^{\phi_2(x)}_{\phi_1(x)}\bigg[\int^{\gamma_2(x,y)}_{\gamma_1(x,y)} f(x,y,z)\,{\it dz}\bigg]\,{\it dy}\bigg\}\,{\it dx}. \]

304

Question 5.98

\(W=\{(x,y,z)\mid \sqrt{x^2+y^2}\leq z\leq 1\}\)

Question 5.99

\(W=\{(x,y,z)\mid \frac{1}{2}\leq z\leq 1\) and \(x^2+y^2+z^2\leq 1\}\)

Question 5.100

\(W=\{(x,y,z)\mid x^2+y^2\leq 1, z\geq 0\) and \(x^2+y^2+z^2\leq 4\}\)

Question 5.101

\(W=\{(x,y,z)\mid |x|\leq 1, |y|\leq 1, z\geq 0\) and \(x^2+y^2+z^2\leq 1\}\)

Question 5.102

Show that the formula using triple integrals for the volume under the graph of a positive function \(f(x,y),\) on an elementary region \(D\) in the plane, reduces to the double integral of \(f\) over \(D\).

Question 5.103

Let \(W\) be the region bounded by the planes \(x=0,y=0,z=0,x+y=1,\) and \(z=x+y\).

(a) Find the volume of \(W\).
(b) Evalute \({\intop\!\!\!\intop\!\!\!\intop}_W x{\it dx}\,{\it dy}\,{\it dz}\).
(c) Evalute \({\intop\!\!\!\intop\!\!\!\intop}_W y{\it dx}\,{\it dy}\,{\it dz}\).

Question 5.104

Let \(f\) be continuous and let \(B_\varepsilon\) be the ball of radius \(\varepsilon\) centered at the point \((x_0,y_0,z_0)\). Let vol (\(B_{\varepsilon}\)) be the volume of \(B_\varepsilon\). Prove that \[ \lim_{\varepsilon \rightarrow 0} \frac{1}{{\rm vol}\, (B_{\varepsilon})}\intop\!\!\!\intop\!\!\!\intop\nolimits_{B_{\varepsilon}} f(x,y,z){\,d} V=f(x_0,y_0,z_0). \]